Estimating Vote Shares

Prices in prediction markets are not probabilities. Nor are they directly proportional to vote shares. But, with enough data about prices and vote shares from past elections, it is possible to estimate vote shares from prediction market prices.

Estimation of two-party vote share is a critical component of The Virtual Tout® forecasting model for 2024. For this we draw on data from the 2020 presidential election. In particular, we draw on prediction market prices and actual voting data from 2020.

PredictIt managed fifty-six (56) prediction markets for the 2020 presidential election. These corresponded to Electoral College voting units or markets. For forty-eight states, there is one winner-take-all market. Maine has three markets. Nebraska has four markets, and there is one market for the District of Columbia.

For our vote share estimation in 2024, we use the winner-take-all, statewide markets for Maine and Nebraska, giving data from 51 prediction markets in 2020. We obtain last-posted prices for the Democratic and Republican tickets in each of these markets on the morning of election day, November 3, 2020. From these prices, we can estimate a normalized Democratic price of winning:

Such a normalized price of winning is assured to take values between zero and one, just as popular two-party vote shares take values between zero and one.

We examine the relationship between the Democratic normalized price of winning on election day and the actual two-party vote share of the Democratic party. We fit a generalized linear model to these data, a model that can then be used to estimate two-party vote shares of the popular vote in future elections, including the presidential election of 2024.

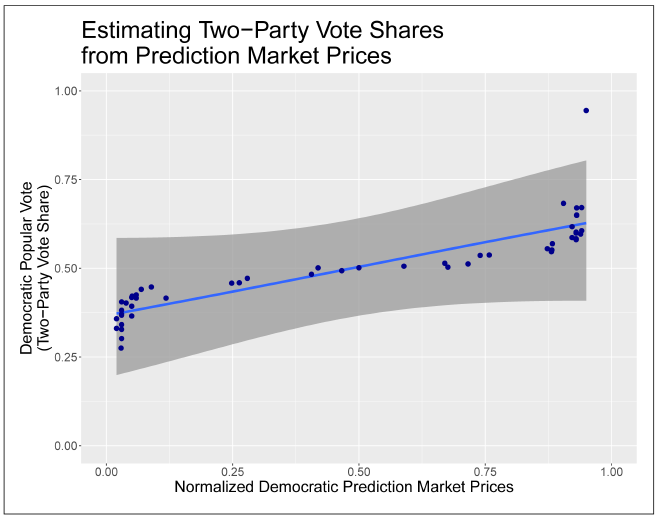
Prediction market prices at both the low and high extremes need to be brought in line with actual vote shares. The generalized linear model fit to these data provides a data-based mechanism for doing this. The resulting two-party vote share estimates can then be used in top-down estimation of Electoral College votes.

Back to Methods.

Go to the home page of The Virtual Tout.